Clearly given f = (r^2)^(n) = r^(2n) where r = sqrt(x^2 y^2 z^2) = r Now as we know that grad(f) = f´(r) (r/r) ==> div(grad(f)) =div(f´(r) r/r)={grad(f · See below Calling Sigma>f(x,y,z)=y^2 3 x^2 z^2 4=0 and considering p = (x,y,z) such that p in Sigma, we have vec n = (pp_1) xx (pp_2) is a vector normal to the plane Pi defined by the points p, p_1, p_2 Now, the vector vec n can be computed over Sigma as grad f = ((partial f)/(partial x), (partial f)/(partial y), (partial f)/(partial z)) =2(3x,y,z) The Sigma tangent · f(x,y,z)=2*e^{8*x*y}2*x^2*y*e^{23*z} Berechnen Sie das totale Differential df Benutzen Sie dabei in Ihrer Lösung die Schreibweise del(x) für den Term dx und analoge Schreibsweisen für andere Variablen Beispielsweise erzeugt der Term 5*x^2*del(x) den Ausdruck 5x2d(x

Factorising Cyclic Expression X 2 Y Z Y 2 Z X Z 2 X Y Youtube
F(x y z x^2 y^2 z^2)=0
F(x y z x^2 y^2 z^2)=0-4 and having density f x y z p x 2 y 2 z 2 The cone z 2 x 2 y 2 z 0 in from MATH 3 at The City College of New York, CUNYZ(x;y;z) = xy 2 z= 0;
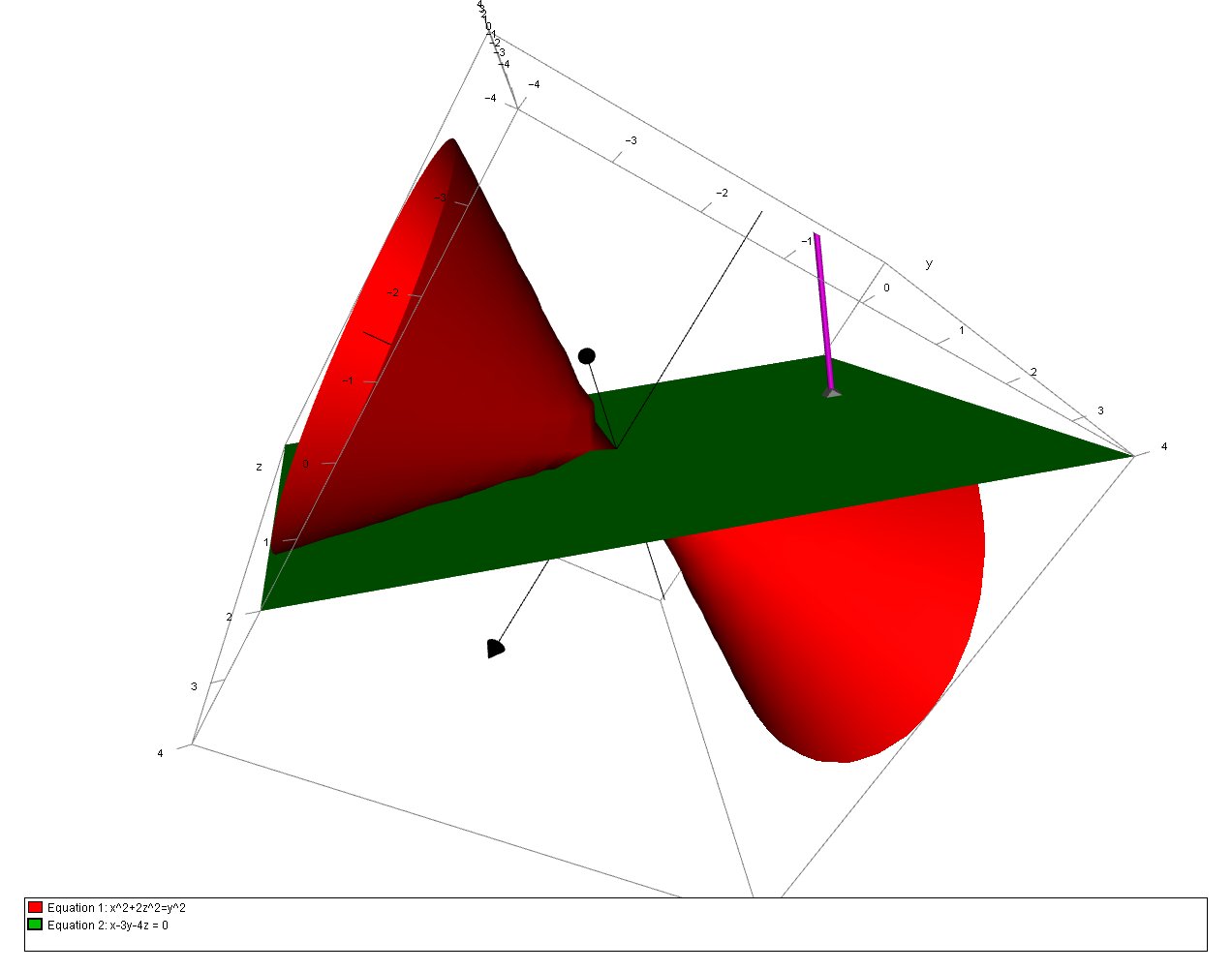


How Do You Find The Equations For The Tangent Plane To The Surface X 2 2z 2 Y 2 Through 1 3 2 Socratic
Click here👆to get an answer to your question ️ If x^2 y^2 z^2 = r^2 , then tan^1 (xy/zr) tan^1 (yz/xr) tan^1 (xz/yr) =设Ω为球面x^2y^2z^2=2z与抛物面z=x^2y^2 1年前 1个回答 音叉 共振 能量守恒音叉共振时,设同一球面及球心中心点上上有无限多个同频率的音叉,振动球心音叉时,球面音叉的都会跟着振动Y^{2}x^{2}z^{2}=0 Quadratic equations like this one, with an x^{2} term but no x term, can still be solved using the quadratic formula, \frac{b±\sqrt{b^{2}4ac}}{2a}, once they are put in standard form ax^{2}bxc=0
And 4z to get x2 = y2 = z2 = 2 Since x2 y2 z2 = 3 2 = 1, we get = 2 3 and thus each of x;y;z is p1 3(\lambda,x,y,z)=2xyz\lambda (3x^2y^2z^2)\ 2) Derive em relação a todas as variáveis e iguale a zero \\fracLetf (x,y,z) = x^2y^2z^2 Calculate the gradient of f Calculate ∫_C (Fdr) where F (x,y,z)= (x,y,z) and C is the curve parametrized by r (t)= (3cos^3 (t), 2sin^5 (t), 2cos^13 (t) for 2π≤t≤3π
· Verify Stokes theorem for F =(y^2 x^2 x^2)i (z^2 x^2 y^2)j (x^2 y^2 z^2)k over the portion of the surface x^2 y^2 2ax az = 0 While evaluating the integral we get hard to evaluate integrals What can we do to simplify this? · 设方程F(xyz,x^2y^2z^2)=0确定了函数 1626 设Z=㏑(根号x根号y),证明:x乘以x的偏导 y乘以 3 已知u=f(x^2y^z^2)求一阶和二阶偏导数Given x^{2}3 x y2 y zy^{2}z^{2}11=0, is an implicit function z=f(x, y) defined around the point (x=1, y=2, z=0) ?



Factorising Cyclic Expression X 2 Y Z Y 2 Z X Z 2 X Y Youtube


Using Properties Of Determinants Prove That X Y Z X 2 Y 2 Z 2 X 3 Y 3 Z 3 Xyz X Y Y Z Z X Sarthaks Econnect Largest Online Education Community
· Verify GDT for vector F = (x^2 yz)vector i (y^2 zx)j (z^2 xy)k taken over the rectangular parallelepiped 0 ≤x ≤ a, 0 ≤ y ≤ b, 0 ≤ z ≤ c · Encontre os pontos que otimizam \(f(x,y,z)=2xyz\) sujeito a \(3x^2 y^2 z^2=0\) Ache os pontos extremos de \(f(x,y)=2xy\) sujeito a \(2x^2y^2=0\) Teste apenas se o ponto extremo positivo \((x>0,y>0)\) é ponto de máximo ou mínimo · Ist f,mit f(x,y,z)= (xyz)/(√(x^2y^2z^2) falls (x,y,z) ≠ (0,0,0) und 0 sonst, stetig bez Euklidischer Metrik?



If X Y Z 0 Then Prove That X 2 Yz Y 2 Zx Z 2 Xy 3 Brainly In



Solve The Following System Of Equation By Matrix Method 1 X Y Z 6 X Y Z 4 X 2y 2z 1 2 X Y 3z 10 X Y Z 2 2x 3y 4z 4 3 X Y Z 6 X 2y 3z 6 X Y Z 2 4 2x Y Mathematics Topperlearning Com Yv1op566
· x^4y^4z^4 = 25/6 Given { (xyz=1), (x^2y^2z^2=2), (x^3y^3z^3=3) } The elementary symmetric polynomials in x, y and z are xyz, xyyzzx and xyz Once we find these, we can construct any symmetric polynomial in x, y and z We are given xyz, so we just need to derive the other two Note that 2(xyyzzx) = (xyz)^2(x^2y^2z^2) = 1 So xyyzzx = 1/2 Note that 6xyz = (xyz6 OM4–VersionduApril1,09 2 Limitesetcontinuité Exercice21 Soitflafonctiondéfiniepar f(x,y) = 2xy−y2 x 2 y Étudier la limite quand (x,y) tend vers (0,0) de la restriction de f à la droite d'équationy= axavecadonnéMontrerquefn'apasdelimiteàl'origine Exercice22 Soitflafonctiondéfiniepar f(x,y) = x2y x4 −2x2y 3y2 si (x,y) 6= 00 si (x,y) = 0i) Étudier la limiteO comprimento e a largura de um retângulo foram medidos como $30$ cm e $24$ cm, respectivamente, com um erro de medida de, no máximo, $0,1$ cm Utilize as diferenciais para estimar o erro máximo cometido no cálculo da área do retângulo



Let Math X 2 Y Z Y 2 Z X Z 2 X Y Math What Is The Value Of Math Frac 1 1 X Frac 1 1 Y Frac 1 1 Z Math Quora



Satyabama Niversity Questions In Vector
· 1 x 2 y 2 z 2 ( x, y, z) ≠ ( 0, 0, 0) 0 ( x, y, z) = ( 0, 0, 0) At first, I study the continuity in the origin I apply the concept of sequential continuity x n → x 0 ⇒ f ( x n) → f ( x 0) So, x n = 1 n x n → 0 ⇒ f ( x n, x n, x n) → f ( 0, 0, 0) = 0 lim n → ∞ 3 n 2 sinPlot f (x,y,z)=x^2y^2z^2 WolframAlpha Assuming "plot" is a plotting function Use as referring to geometry · How can I use Matlab to plot theses two plans X^2Y^2Z^2=0 and F 2 ax^2bY^2Z^2=0 Knut J 0 Comments Show Hide 1 older comments Sign in to comment Sign in to answer this question Accepted Answer bym on 30 May 11 Vote 0 Link



Solutions To Homework Assignment 4 Math 253
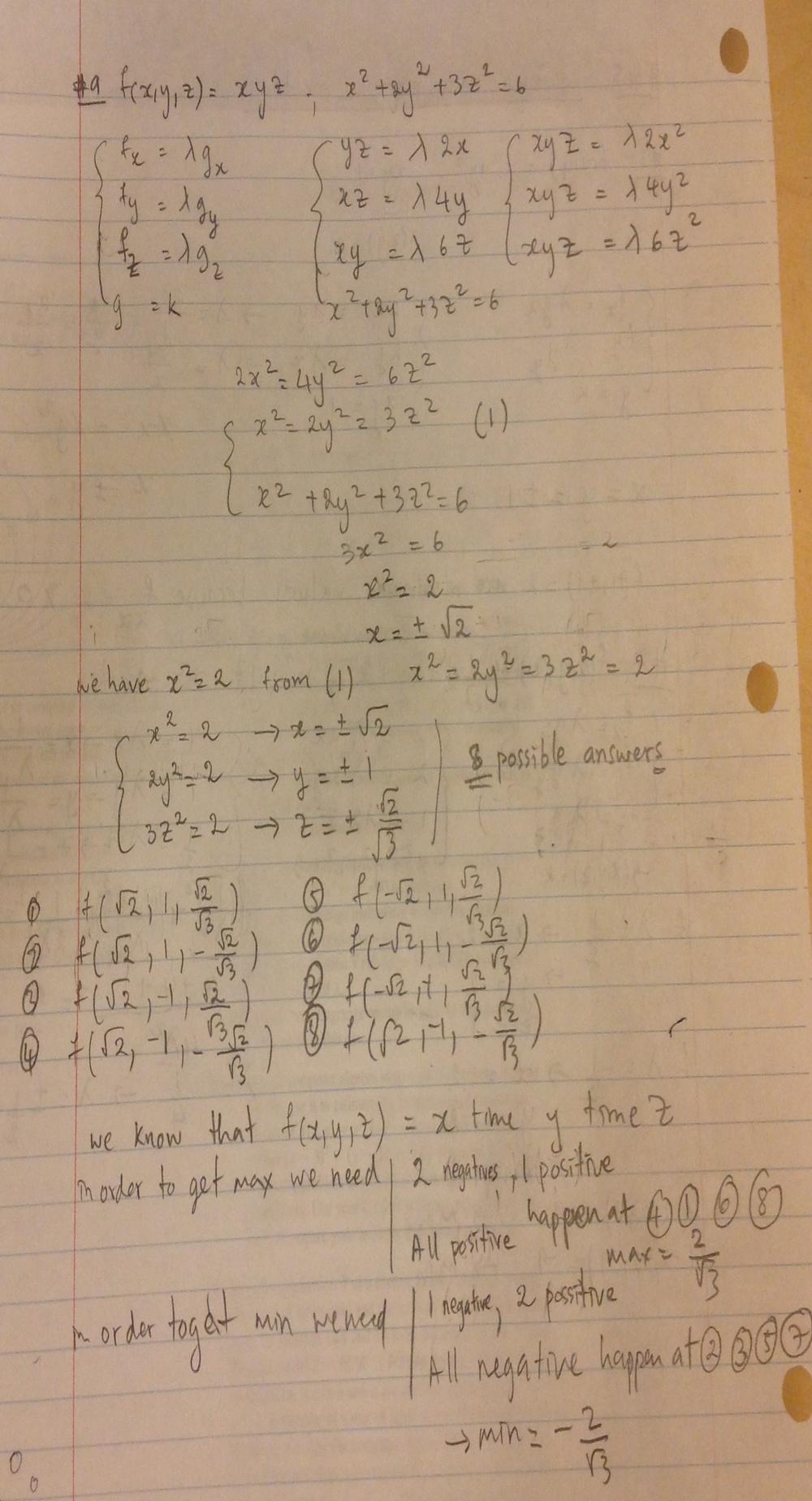


Use Lagrange Multipliers To Find The Maximum And Minimum Values Of The Function Subject To The Given Constraint F X Y Z Xyz X 2 2y 2 3z 2 6 Homework Help And Answers Slader
3Dplot of "x^2y^2z^2=1" Learn more about isosurface;The Roman surface or Steiner surface is a selfintersecting mapping of the real projective plane into threedimensional space, with an unusually high degree of symmetryThis mapping is not an immersion of the projective plane; · f(0,0,0) is 0, not 1 (the isosurface level), so you only get points drawn completing the cones if there are enough points near the origin that happen to have value 1 But when you switch to linspace(,,), the closest coordinates to the origin are at about 105, leaving a gap of about 21 between adjacent points



How Do You Find The Equations For The Tangent Plane To The Surface X 2 2z 2 Y 2 Through 1 3 2 Socratic



Math 6c Chapter 12 Quiz
F (x) = (x y z) {x 2 − (y z) x (y 2 − y z z 2)} = (x y z) (x 2 y 2 z 2 − x y − y z − z x) ホーム>>カテゴリー別分類>>数と式>>整式:因数分解の公式 (xyz)(x^2y^2z^2xyyzzx) 最終更新日: 14年9月9日CurlF ydS, for F(x;y;z) = 2ycosziexsinzjxek, where Sis the hemisphere x2y2z2 = 9, z 0, oriented upward The boundary curve Cof Sis the circle x 2 y 2 = 9, z= 0, oriented counterclockwise looking downMinimize the function f(x, y, z)=x^{2}y^{2}z^{2} subject to the constraints x2 y3 z=6 and x3 y9 z=9 Video Transcript So the question is gonna look a little bit different We instead of having one constraints, we're gonna find extreme value


Solved Maximizing A Product Find The Largest Prod



Integrate F X Y Z xz Over The Region In The First Octant X Y Z 0 Above The Parabolic Cylinder Brainly Com
ZadaniazAnalizyMatematycznejII Seria3 1 Dla0 < x < 1 policzyćcałkę Z 1 0 xfidfi 2 Wykazać,żefunkcja f(x) = 1 ¡lnx dla 0 < x < 1; · Encontre os pontos que otimizam \(f(x,y,z)=2xyz\) sujeito a \(3x^2 y^2 z^2=0\) 0 votos 645 visitas perguntada Jan 26, 16 em Matemática por danielcajueiro (5,566 pontos) otimizaçãocomrestrição;If s 0, find \partial z / \partial x and



Find The Product X Y Z X 2 Y 2 Z 2 Xy Yz Zx Youtube
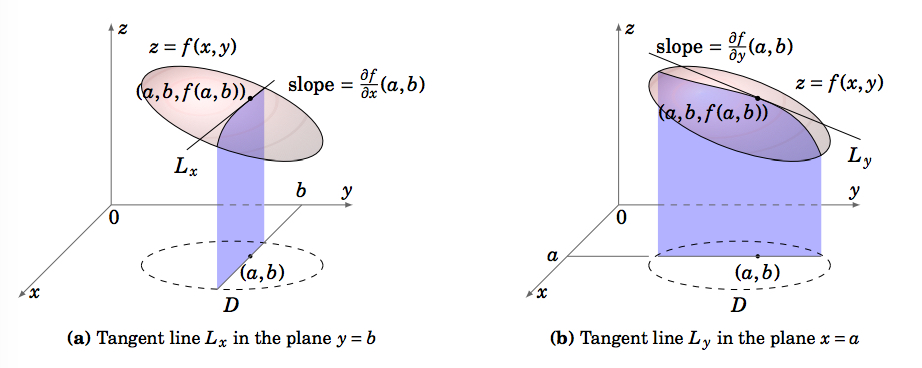


2 3 Tangent Plane To A Surface Mathematics Libretexts
· 设z=z(x,y)由x^2y^2z^24z=0确定 则 4 1522 设z=z(x,y)由x22y2z24x2z5=0确 5 设函数z=f(x,y)由方程x2y2z22z6=0,3dprinting, solidworks f(0,0,0) is 0, not 1 (the isosurface level), so you only get points drawn completing the cones if there are enough points near the origin that happen to have value 1 But when you switch to linspace(,,), the closest coordinates to the origin are at about 105, leaving a gap of about 21 between adjacentHowever, the figure resulting from removing six singular points is one Its name arises because it was discovered by Jakob Steiner when he was in Rome in 1844



Chapter 16 1 16 3 Solutions Rogowski Pdf Document



Calc 501 1000 By James Bardo Issuu
1 (Exercise 12) Find the maximum and minimum of f(x;y;z) = x4 y4 z4 subject to the constraint x 2y2 z = 1 Solution We have ∇f(x;y;z) = 4x3;4y3;4z3 = 2 x;2 y;2 z = ∇g(x;y;z) Case 1 If all of x;y;z ̸= 0, we can divide 4x3 = 2 x, 4y3 = 2 y, 4z3 = 2 z by 4x;4y;If F = ( x 2, y 2, z 2), S = { x 2 y 2 z 2 = 1, z ≥ 0 }, evaluate ∬ S F d S I'm having trouble computing this In spherical coordinates we get which is really hard to evaluate But we know that the normal vector to the sphere is r = ( x, y, z), hence, Can we say that the first summand evaluates to zero since S is symmetrical with respect toBy x > 0, z > 0, y > 3x, and 9 > y2 z2 Solution Recall I = Z 1 0 Z 3 3x Z √ 9−y2 0 z dz dy dx We now compute the integral ZZZ D f dv = Z 1 0 Z 3 3x z2 2 9 √ −y2 0 dy dx, = 1 2 Z 1 0 Z 3 3x (9 − y2)dy dx, = 1 2 Z 1 0 h 9 y 3 3x − y3 3 3 3x i dx Triple integrals in arbitrary domains Example Compute the triple integral of f (x



Oneclass Use Lagrange Multipliers To Find The Maximum And Minimum Values Of F X Y Z X2 8y 10z2 Subj



17 Given F X Y Z X Yz Xyz P 2 1 1 And Vector V 1 0 1 Find Homeworklib
'(x;y) = x 2y2 z 3 = 0 Multiplizieren wir die ersten drei Gleichungen mit x, ybzw z, so folgt xyz= 2 x 2= 2 y = 2 z2 Damit erhalten wir (x2 y2) = (x 2 z2) = (y2 z) = 0, also x 2= y = z = 1;Advertisement Remove all ads If U = F ( Y − X X Y , Z − X X Z ) , Show that X 2 ∂ U ∂ X Y 2 ∂ U ∂ Y Z 2 ∂ U ∂ Z = 0 Applied Mathematics 1 Sum If u =`f ( (yx)/ (xy), (zx)/ (xz)),` show that `x^2 (delu)/ (delx)y^2 (delu)/ (dely)z^2 (delu)/ (delz)=0` Advertisement Remove all adsSolutionGiven x2 y2 z2 −xy −yz−zx= 02x2 2y2 2z2 −2xy−2yz−2zx = 0(x2 −2xyy2)(y2 −2yzz2)(z2 −2zxx2) = 0⇒ (xy)2 (y−z)2 (z−x)2 = 0⇒ x = y = z = k⇒ zxy = k2k =2



Solved Evaluate Tripleintegral B E X 2 Y 2 Z 2 3 2 W Chegg Com


Lagrange Multipliers Minimum Of F X Y Z X 2 Y 2 Z 2 Subject To X Y Z 9 0 Youtube
Answer to let f(x,y,z) = xyz/(x2 y2z2)a if (x,y,z) not =(0,0,0) 0 if (x,y,z) = (0,0,0) where a is a constant show that f is dif · Viewed 2k times 1 0 The problem is I have to find all the possible combination of integers (x, y, z) that will satisfy the equation x^2 y^2 z^2 = N when you are given an integer N You have to find all the unique tuples (x, y, z) For example, if one of the tuple is (1, 2, 1), then (2, 1, 1) is not unique anymore= 1 2 denn wegen 3xyz= 2 x2 y2 z2 = 6 erhalten wir für = 0 sicher keine globalen Extremstellen Siehe nächstes Blatt!
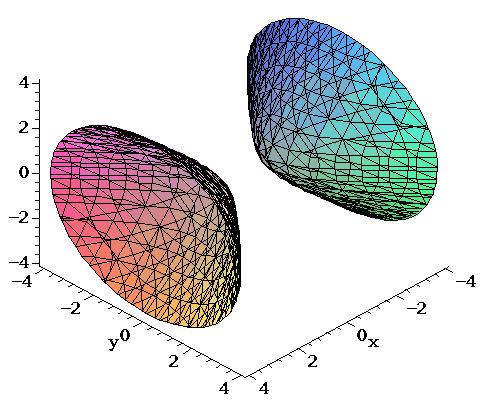


Surfaces Part 2



X3 Y3 Z3 3xyz X Y Z X2 Y2 Z2 Xy Yz Zx Proof It Lhs To Rhs Brainly In
0 dla x • 0F(x, y, z, p, q ) = 0 Example 5 Obtain the partial differential equation by eliminating „f„from z = ( xy ) f ( x 2 y 2 ) Let us now consider the equation z = (xy ) f(x 2 y 2) _____ (1) Differentiating (1) partially wrt x & y , we get p = ( x y ) f ' ( x 2 y 2 ) 2x f ( x 2 y 2 ) q = ( x y ) f ' ( x 2 y 2Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science



Matlab Tutorial
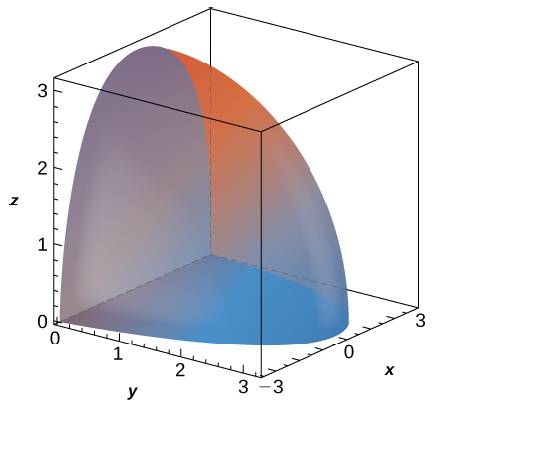


270 F X Y Z 1 X 2 Y 2 Z 2 B X Y Z X 2 Y 2 Z 2 9 Y 0 Z 0 Bartleby
XYZ= 1, X^2Y^2Z^2=2 , X^3Y^3Z^3=3 find X^5Y^5Z^5 Watch later Share Copy link Info Shopping Tap to unmute If playback doesn't begin shortly, try restarting your device Up · $f(x,y,z)=e^{x^2y^2z^2}$ kuralı ile verilen $f\mathbb{R}^3\rightarrow \mathbb{R}$ fonksiyonunun sürekli olduğunu gösteriniz2806 · f(x,y)=(x^2y^2)/x = 0 Learn more about 3d plots, homework
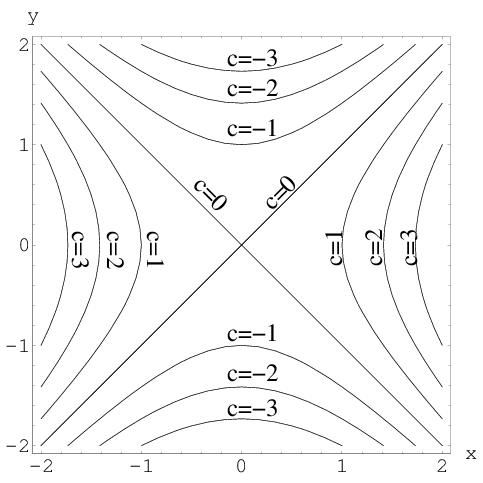


Level Set Examples Math Insight



Unit 2
Calculus Multivariable Calculus Find the work done by the force field F ( x , y , z ) = x− y 2 , y − z 2 , z − x 2 on a particle that moves along the line segment from (0, 0, 1) to (2, 1, 0)Answer to Let f(x,y,z)=x^2y^2z^2 and let S be the level surface defined by f(x,y,z) = 4 (a) Find an equation for the plane tangent to S for Teachers for Schools for Working Scholars® forY^ {2}x^ {2}z=0 Quadratic equations like this one, with an x^ {2} term but no x term, can still be solved using the quadratic formula, \frac {b±\sqrt {b^ {2}4ac}} {2a}, once they are put in standard form ax^ {2}bxc=0 y=\frac {0±\sqrt {0^ {2}4\left (x^ {2}z\right)}} {2}
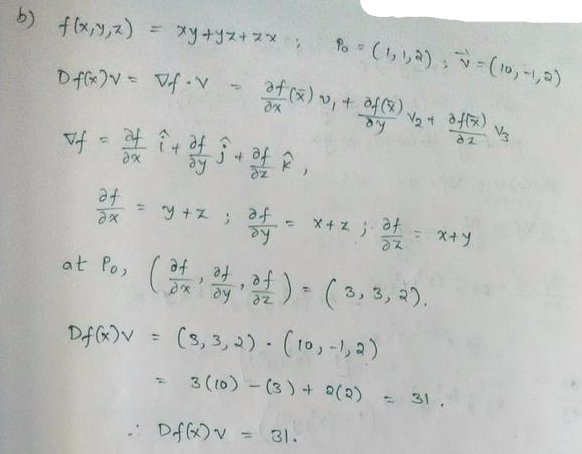


Find The Directional Derivative Of The Given Function At The Given Point And In The Direction Of The Given Vector A Math F X Y Z E X Cos Yz P 0 0



Solutions To Assignment 7


The Divergence Theorem Page 2


What Is The Unit Normal To The Surface Xy Yz Zx 3 Of The Point 1 1 1 Quora



32 Approximation Of Eg6 Shrek F X Y Z X 4 Y 4 Z 4 4 X 2 Download Scientific Diagram



If X 2 Y 2 Z 2 R 2 And X Y Z 0 Then Tan 1 Xy Z
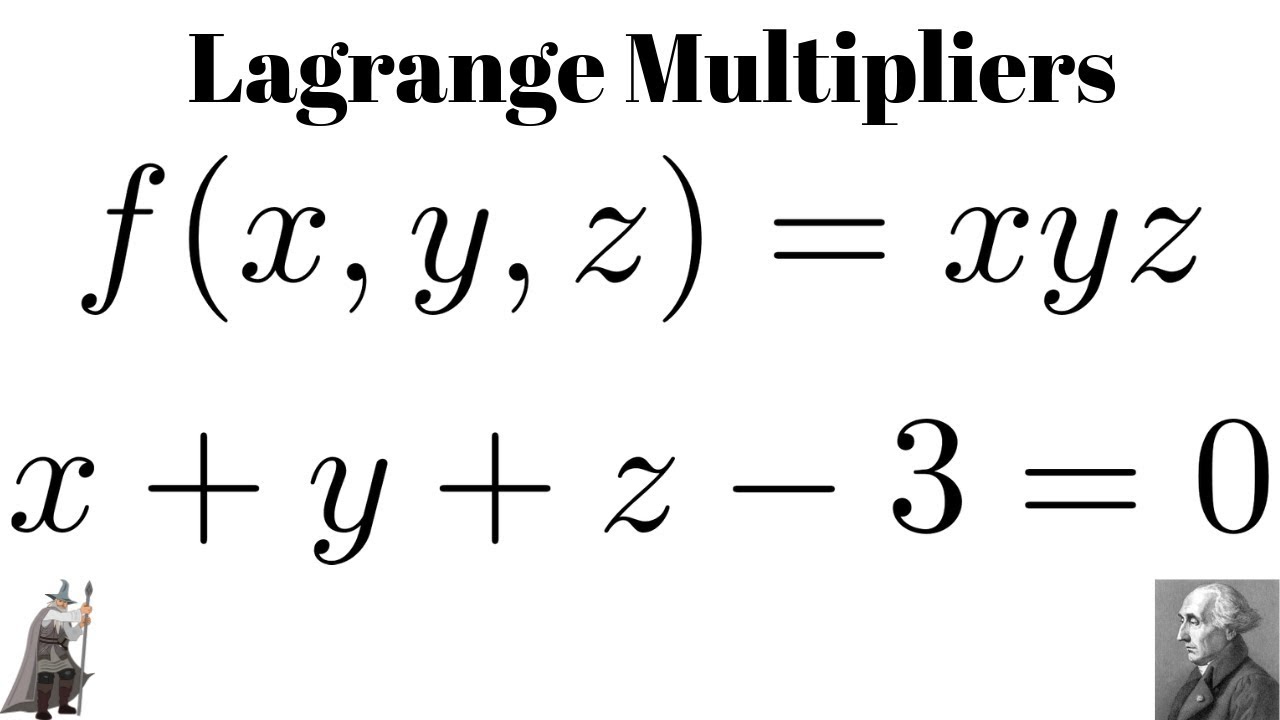


Lagrange Multipliers Maximum Of F X Y Z Xyz Subject To X Y Z 3 0 Youtube



Ex 4 2 9 Show That X X2 Yz Y Y2 Zx Z Z2 Xy X Y Y Z


How To Prove That Math X Y Z 3 27xyz Geq0 Math Quora
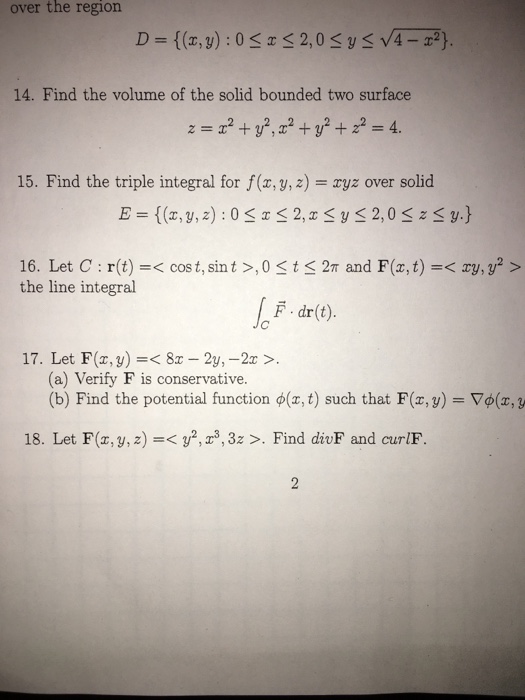


Solved 14 Find The Volume Of The Solid Bounded By Two S Chegg Com
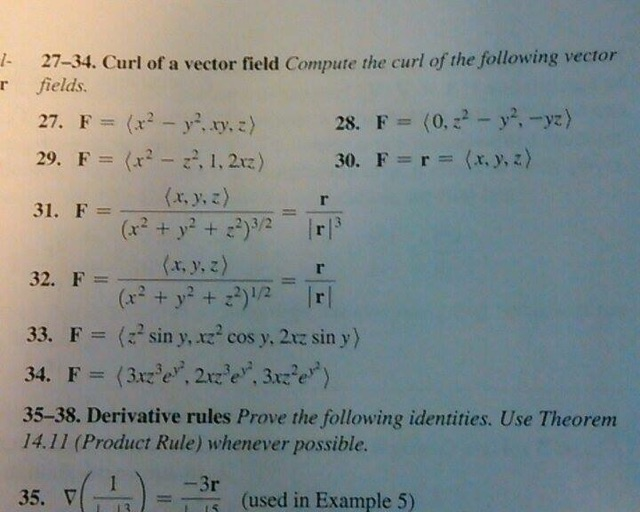


Solved Curl Of A Vector Field Compute The Curl Of The Fal Chegg Com



Maxiam Minima With Side Condition Maxima And Minima Analysis
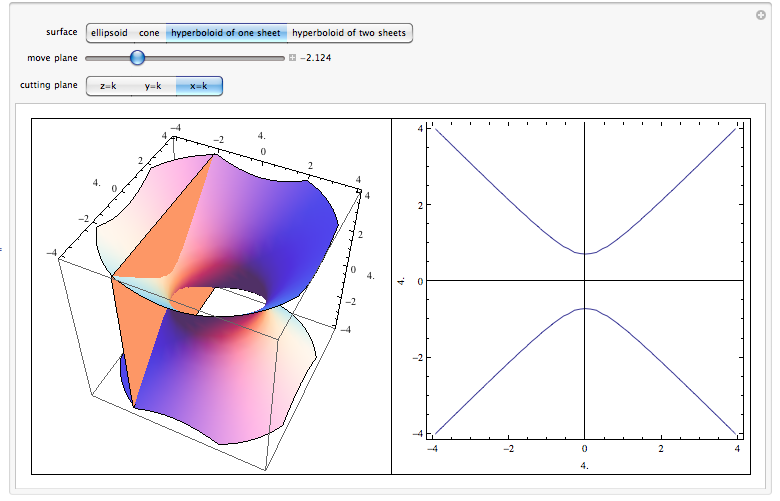


Level Surfaces



Partial Derivative Of F X Y Z With Respect To Z Mathematics Stack Exchange



How Is Frac Dx Z X Y Frac Dy Z X Y Frac Dz X 2 Y 2 Equivalent To Frac Y Dx Xdy Zdz 0 Frac Xdx Ydy Zdz 0 Mathematics Stack Exchange



How Do I Graph Z Sqrt X 2 Y 2 1 Without Using Graphing Devices Mathematics Stack Exchange


Surface Area
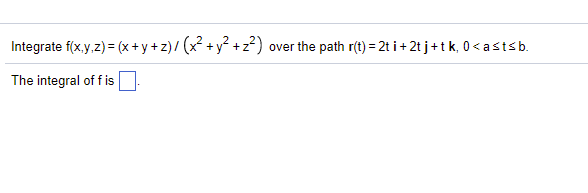


Solved Integrate F X Yz X Y Z X2 Y2 Z2 Over Chegg Com



Solved Describe The Domain Of The Function F In Words A Chegg Com



Solved Finding An Equation Of A Tangent Plane In Exercise Chegg Com



X Y Z Belong To R X Y Z 4 X 2 Y 2 Z 2 6 Find Maximum Possible Value Of Z Mathematics Topperlearning Com 2j1z7sww



Vector Analysis By Alimkanwalimtinaa Issuu
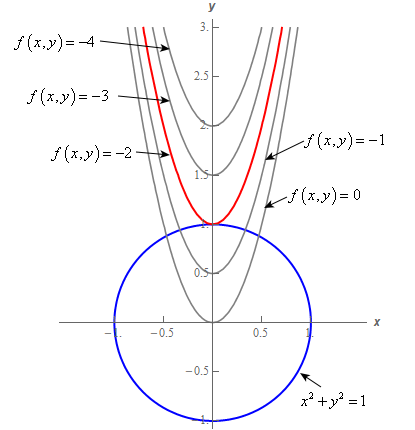


Calculus Iii Lagrange Multipliers
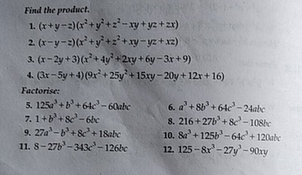


Find The Product 1 X Y Z X2 Y2 Z2 Xy Yz Zx 4 Gr Scholr



Solved Find The Average Value Of F X Y Z Xyz Over X2 Chegg Com



1 9 3 We Would Like To Make The Length 6 The Only Vectors In The Same Direction As V Are Those Pdf Free Download



Unit 2


Surface Area



Solved In Exercises 5 16 Use The Divergence Theorem To E Chegg Com



Surfaces Part 2



Thomas Calculus 11e 1263 1564 Pages 151 0 Flip Pdf Download Fliphtml5
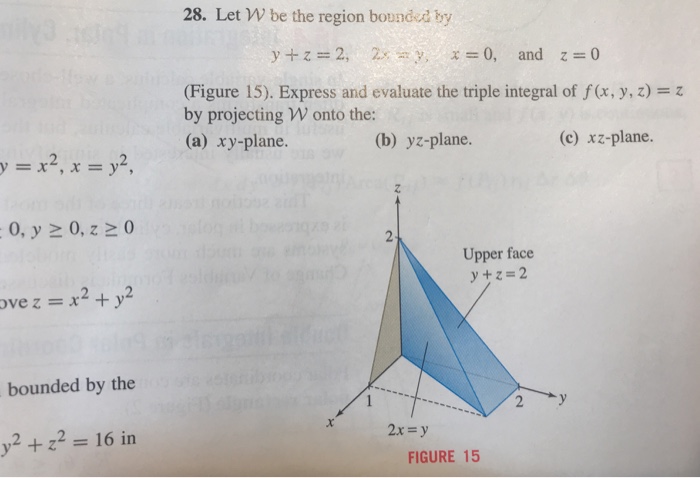


Solved 28 Let W Be The Region Bounded By Y Z 2 2x Y X Chegg Com
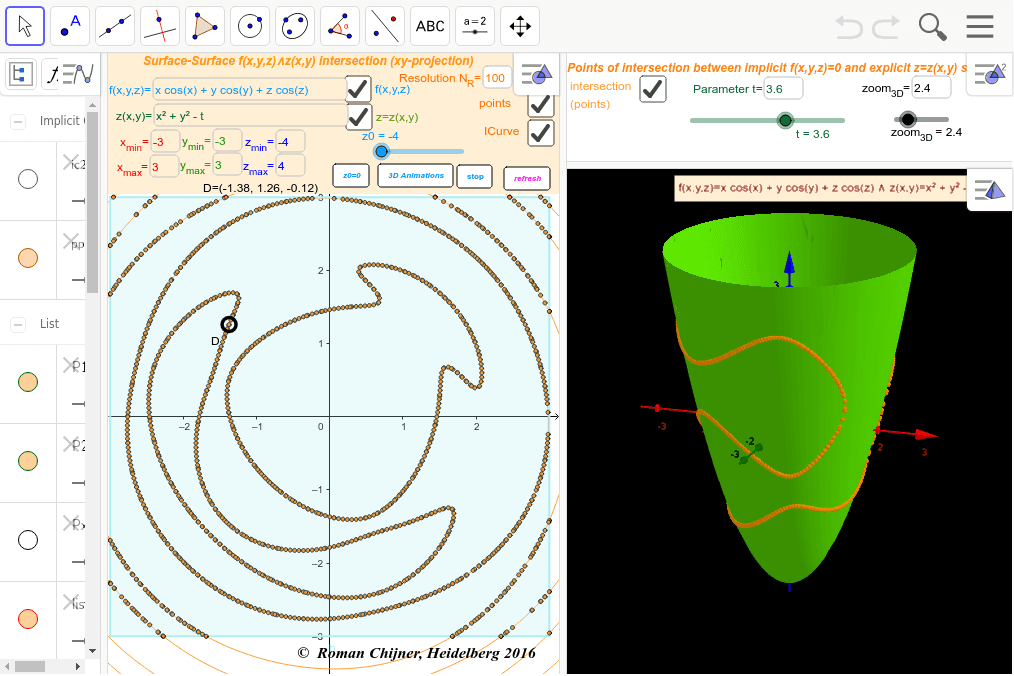


Points Of Intersection Between Implicit F X Y Z 0 And Explicit Z Z X Y Surfaces Geogebra
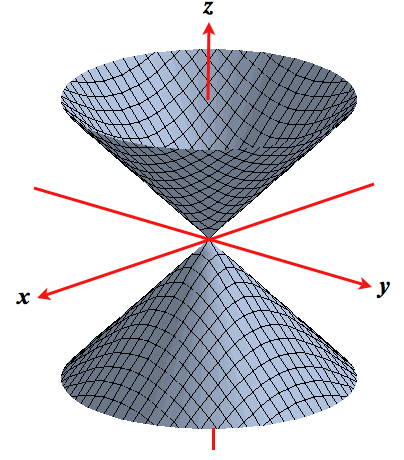


Level Surfaces



If X 2 Y 2 Z 2 1 Then Xy Yz Zx Lies In
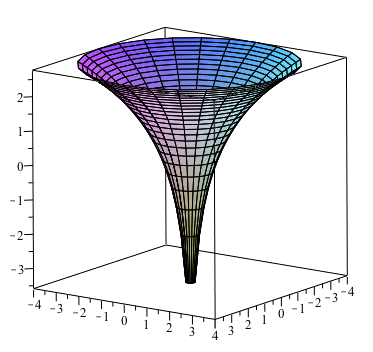


How Do You Sketch F X Y Ln X 2 Y 2 Socratic
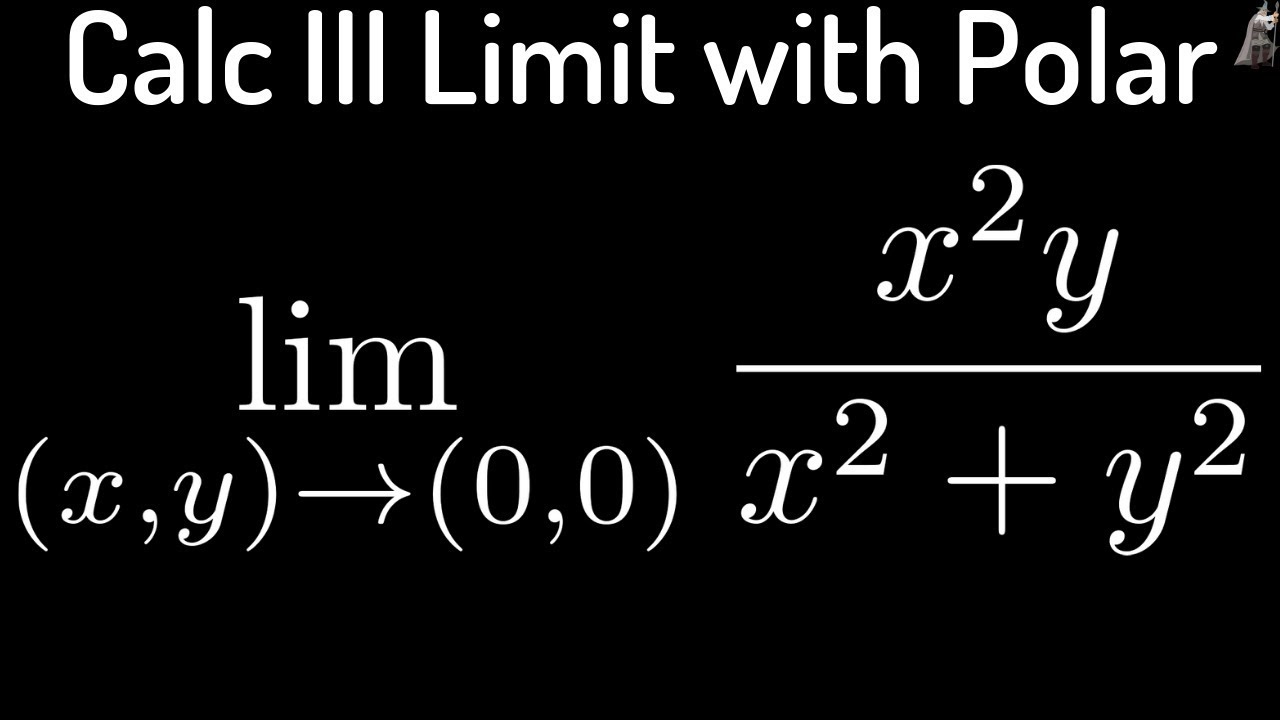


Multivariable Calculus Limit Of X 2y X 2 Y 2 Using Polar Coordinates Youtube


Math Help



Answered 9 M A Y Z Xyz Xyz P 2 1 1 U Bartleby



Matlab Tutorial



Graphs Of Surfaces Z F X Y Contour Curves Continuity And Limits


If X 2 Y 2 Z 2 2 X Y Z 3 What Is The Value Of 2x 3y 4z Quora



Solve A System Of Non Linear Equation Docx


Examples Wednesday Feb 19


Using Properties Of Determinants Prove That X 2 1 Xy Xz Xy Y 2 1 Yz Xz Yz Z 2 1 1 X 2 Y 2 Z 2 Sarthaks Econnect Largest Online Education Community



Lagrange Multipliers By Rohit Venkat Ppt Video Online Download



Answered 14 F X Y Z X Y 4z X Y Bartleby



Tangent Plane To X 2 Xy Y 2 Z 0 Youtube


Solved 6 Find The Maximum Value Of The Function F X Y Z Xyz On The Sphere X2 Y2 Z2 12 8 4 0 4 8 None Of These Rm 9 0 9 S 7 Maximi Course Hero



The Cubic X 2 Y 2 Z 2 2 Xyz 1 0 Download Scientific Diagram
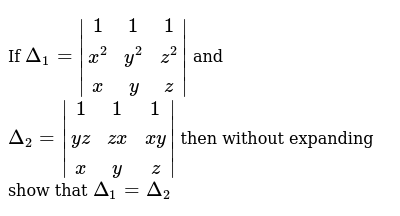


If Delta 1 1 1 1 X 2 Y 2 Z 2 X Y Z And Delta 2 1
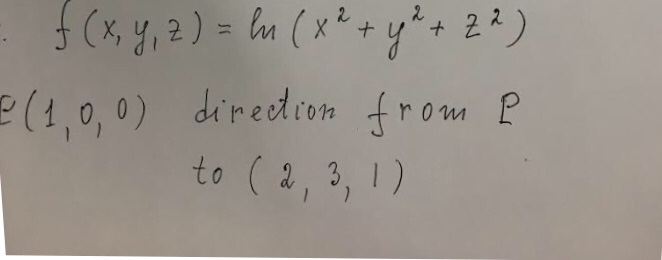


Solved F X Y Z Ln X 2 Y 2 Z 2 1 0 0 Direct Chegg Com



Consider Minimizing And Or Maximizing A Function Z F X Y Subject To A Constraint G X Y C Y Z X Z F X Y Parametrize The Curve Defined By G X Y Ppt Download


Surface Area


What Is The Graph Of X 2 Y 2 Z 2 1 Quora



Ex 4 2 9 Show That X X2 Yz Y Y2 Zx Z Z2 Xy X Y Y Z


Using Matrix Method Solve The System Of Equations 3x 2y 2z 3 X 2y 3z 6 2x Y Z 2 Studyrankersonline



0 件のコメント:
コメントを投稿